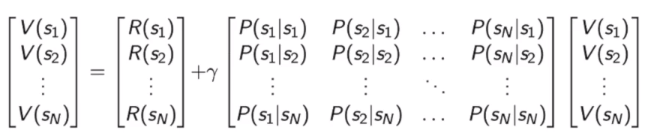强化学习基础和马尔科夫决策过程

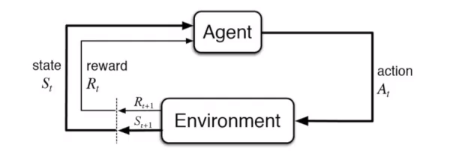
强化学习基本过程

强化学习基本要素

• 模型
• 政策
• 价值

深度学习不同点

• 没有标签，只有反馈
• 学习的过程来自于试错
• 学习的反馈有延迟
• 动作会影响数据
• 观察数据有时间的关联

马尔科夫基本过程（MDP）

马尔科夫过程的下一状态只取决于当前状态

马尔科夫奖励过程

• S：state
• R: Reward,$R(s_t=s)$
• Discount factor $\gamma \in [0,1]$
• P:dynamics/transition model

Horizon

• Number of maximum time steps in each episode
• Can be infinite,otherwise called finite Markov (reward) Process

Return

$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}...{\gamma }^{T-t-1}{R}_T$$

可以看出随着时间变化，奖励值会衰减，只有离开某个状态才能获得奖励，所以奖励来自于未来的状态

state value function Vt(s) for a MRP

Expected

$$\begin{gathered} V_t(s)=E[G_t|s_t=s] \\ =E[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}...{\gamma }^{T-t-1}{R}_T|s_t=s] \end{gathered}$$

Discount Factor $\gamma$

可以作为强化学习的超参数调整

• 当$\gamma =0$，奖励只取决于当前状态

Bellman equation

Bellman方程描述了状态的迭代关系

$$V(s)=R(s)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s)V(s^{\prime })$$

也可以写为矩阵的形式

我们可以通过矩阵求逆的过程求出V

$$\begin{gathered} V=R+\gamma PV \\ \to V=(1-\gamma P{)}^{-1}R \end{gathered}$$

矩阵求逆的计算量太大，所以我们一般用迭代的方法求解

• 动态规划法
• 蒙特卡洛采样法
• Temporal-Difference learning

蒙特卡洛法

动态规划

马尔科夫决策过程

增加了一个动作

• S：state
• A: action
• R: Reward,$R(s_t=s)$
• Discount factor $\gamma \in [0,1]$
• P:dynamics/transition model $P(s_{t+1}=s^{\prime }|s_t=s,a_t=a$

Policy

• policy决定了当前采取的策略
• Policy：$\pi (a|s)=P(a_t=a|a_t=s)$
• Policies are stationary (time-independent)，$A_t～\pi (a|s)$ for any t > 0

• Given an MDP $(S,A,P,R,\gamma )$ and a policy $\pi$
• The state sequence S1, S2,… is a Markov process $(S,P^{\pi })$
• The state and reward sequence S1,R2,S2, R2,… is a Markov reward
  process (S, PT,R”, ) where,

$$\begin{gathered} P^{\pi }(s^{\prime }\mid s)=\sum _{a\in A}\pi (a\mid s)P(s^{\prime }\mid s,a) \\ {R}^{\pi }(s)=\sum _{a\in A}\pi (a\mid s)R(s,a) \end{gathered}$$

当policy$\pi$已知时，马尔科夫决策过程会转化为马尔科夫奖励过程

马尔科夫决策过程的下一状态先由当前状态采取的决策决定

State Value Function

$$v^{\pi }(s)={\mathbb{E}}_{\pi }[G_t\mid s_t=s]$$

action-value function

$$q^{\pi }(s,a)={\mathbb{E}}_{\pi }[G_t\mid s_t=s,A_t=a]$$

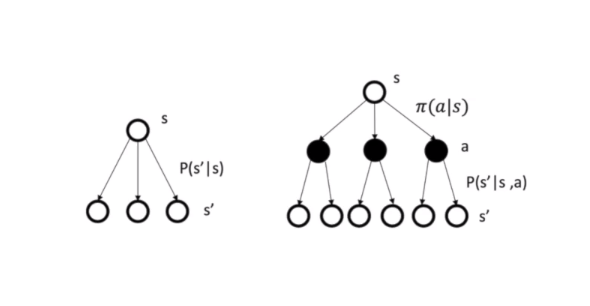
状态价值函数和动作价值函数的关系

$$v^{\pi }(s)=\sum _{a\in A}\pi (a\mid s)q^{\pi }(s,a)$$

Bellman Equation

$$\begin{gathered} v^{\pi }(s)=E_{\pi }[R_{t+1}+\gamma v^{\pi }\left(s_{t+1}\right)\mid s_t=s] \\ =\sum _{a\in A}\pi (a\mid s)q^{\pi }(s,a) \\ =\sum _{a\in A}\pi (a\mid s)(R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }\mid s,a)v^{\pi }\left(s^{\prime }\right)) \end{gathered}$$

---

$$\begin{gathered} q^{\pi }(s,a)=E_{\pi }[R_{t+1}+\gamma q^{\pi }(s_{t+1},A_{t+1})\mid s_t=s,A_t=a] \\ =R_s^a+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }\mid s,a)v^{\pi }\left(s^{\prime }\right) \\ =R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }\mid s,a)\sum _{a^{\prime }\in A}\pi (a^{\prime }\mid s^{\prime })q^{\pi }(s^{\prime },a^{\prime }) \end{gathered}$$

$v^{\pi }$表示了采用policy$\pi$得到奖励的期望

马尔科夫决策过程的预测和控制

• 预测
  • 预测价值
• 控制
  • 寻找最佳策略

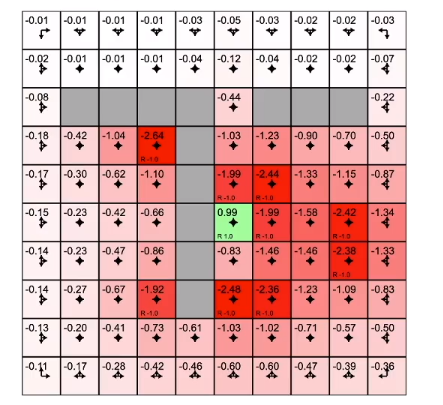
predition

尝试所有策略，收敛后得到价值函数

optimal value function and policy

$$\begin{gathered} v^{\ast }(s)=ma{x}_{\pi }{v}^{\pi }(s) \\ {\pi }^{\ast }(s)=argma{x}_{\pi }{v}^{\pi }(s) \end{gathered}$$

如何寻找最佳的policy?
最佳行为可以定义为

$${\pi }^{\ast }(a\mid s)=\{\begin{array}{ll}1,& \text{ if }a=\arg \underset{a\in A}{max}{q}^{\ast }(s,a)\\ 0,& \text{ otherwise }\end{array}$$

policy search

策略搜索的方法主要有以下两种

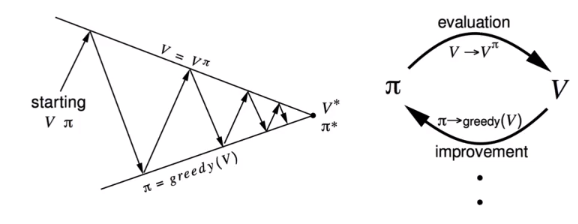
policy iteration

策略迭代算法有两个步骤

• 估计当前政策价值函数
• 采用贪心算法改进策略

$${\pi }^{\prime }=greedy(v^{\pi })$$

policy improvwment

• 计算当前策略价值$$q^{{\pi }_i}(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }\mid s,a)v^{{\pi }_i}\left(s^{\prime }\right)$$
• 计算新政策价值$${\pi }_{i+1}(s)=\underset{a}{\arg max}{q}^{{\pi }_i}(s,a)$$

$$q^{\pi }(s,{\pi }^{\prime }(s))=\underset{a\in A}{max}{q}^{\pi }(s,a)$$

value iteration

$$v(s)=\underset{a\in A}{max}(R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }\mid s,a)v\left(s^{\prime }\right))$$